前言

上篇文章介绍了使用matplotlib绘制折线图，参考：https://www.jb51.net/article/198991.htm，本篇文章继续介绍使用matplotlib绘制散点图。

一、matplotlib绘制散点图

# coding=utf-8
import matplotlib.pyplot as plt


years = [2009, 2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019]
turnovers = [0.5, 9.36, 52, 191, 350, 571, 912, 1027, 1682, 2135, 2684]
plt.figure(figsize=(10, 10), dpi=100)
plt.scatter(years, turnovers)
plt.show()

运行结果：

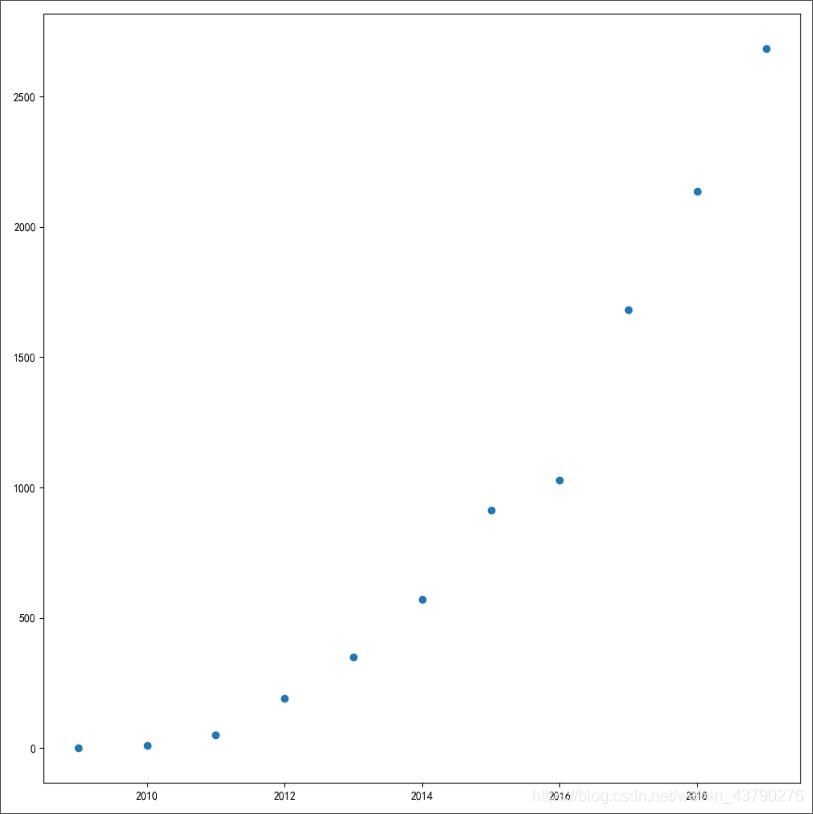
scatter(): matplotlib中绘制散点图的函数。可以传入很多参数，一般传入两个列表，分别是散点图中的x值和y值。上面的例子中使用2009年至2019年这十一年天猫双11的总成交额数据。

散点图根据提供的两组数据，构成图形中的多个坐标点。根据坐标点的分布，分析两个变量之间是否存在某种关联，或总结坐标点的分布趋势，用于预测数据的走势。

上面的代码已经实现了简单的散点图，但只把点绘制出来了，很多信息都不完整，所以需要进行优化。

二、matplotlib优化散点图

import matplotlib.pyplot as plt


years = [2009, 2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019]
turnovers = [0.5, 9.36, 52, 191, 350, 571, 912, 1027, 1682, 2135, 2684]
plt.figure(figsize=(10, 15), dpi=100)
plt.scatter(years, turnovers, c='red', s=100, label='成交额')
plt.xticks(range(2008, 2020, 1))
plt.yticks(range(0, 3200, 200))
plt.xlabel("年份", fontdict={'size': 16})
plt.ylabel("成交额", fontdict={'size': 16})
plt.title("历年天猫双11总成交额", fontdict={'size': 20})
plt.legend(loc='best')
plt.show()

运行结果：

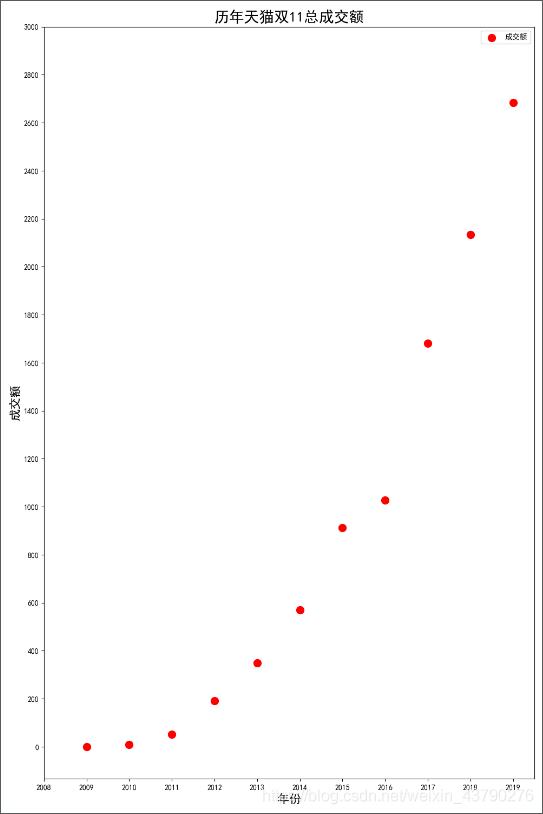
在第一次绘制的散点图中，已经看出了点的大概分布情况，所以在使用figure()函数创建图像时，可以修改figsize参数调整图像尺寸，设置更好的图像比例。

在调用scatter()函数绘制散点图时，使用c='颜色'来设置点的颜色，使用s='大小'来设置点的大小，并设置label用于图例展示。

第一次的散点图中，x轴上没有显示所有的年份刻度，最后一个点已经分布到了图形的右上角，所以使用xticks()和yticks()来设置x轴和y轴的刻度标签和范围。

使用xlabel()和ylabel()设置x轴和y轴的标签，说明x轴和y轴的含义。使用title()设置散点图的标题，说明散点图展示的数据。使用legend()将图例展示出来。

这样一张基本功能完整，信息完整的散点图就完成了。

三、matplotlib散点图区分点的颜色和大小

import matplotlib.pyplot as plt
import numpy as np


years = [2009, 2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019]
turnovers = [0.5, 9.36, 52, 191, 350, 571, 912, 1027, 1682, 2135, 2684]
plt.figure(figsize=(10, 15), dpi=100)
size = list()
for tur in turnovers:
 size.append(tur) if tur > 100 else size.append(100)
plt.xticks(range(2008, 2020, 1))
plt.yticks(range(0, 3200, 200))
plt.scatter(years, turnovers, c=np.random.randint(0, 50, 11), s=size)
plt.xlabel("年份", fontdict={'size': 16})
plt.ylabel("成交额", fontdict={'size': 16})
plt.title("历年天猫双11总成交额", fontdict={'size': 20})
plt.show()

运行结果：

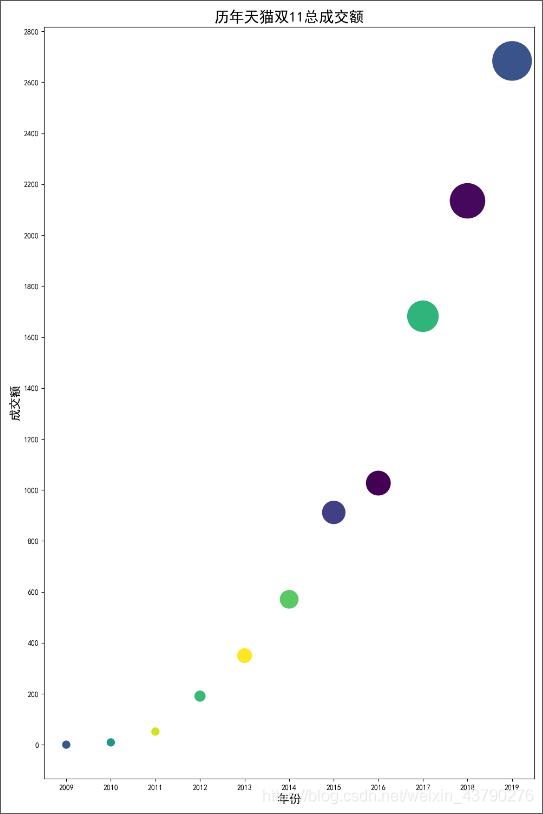
上一张散点图中已经对数据作了基本的展示，为了使数据展示效果更好，可以对散点图进行美化。

数据是历年双11的总成交额，每年的数据是独立的，可以用不同的颜色来区分。这里使用numpy中的random.randint()随机生成11个值，将这11个随机的值传给scatter()函数中的c参数，使每一个点的颜色不一样，可以更好地表示每个点的独立性。

pip install numpy -i https://pypi.tuna.tsinghua.edu.cn/simple

成交额是逐年变化的，为了从散点图中体现出大小的差异，可以根据成交额的大小设置点的大小。这里直接将成交额作为点的大小(成交额很小的设置一个值，图形中的点不小于这个值)，得到由11个值组成的列表，传给scatter()函数中的s参数，可以体现每个点的大小差异(成交额越大点越大)。

四、matplotlib散点图的趋势简单分析

import matplotlib.pyplot as plt
import numpy as np
import math


years = [2009, 2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019]
turnovers = [0.5, 9.36, 52, 191, 350, 571, 912, 1027, 1682, 2135, 2684]
squares = [math.pow(year-2008, 3.3) for year in years]
powers = [math.pow(2, year-2008) for year in years]
plt.figure(figsize=(10, 15), dpi=100)
size = list()
for tur in turnovers:
 size.append(tur) if tur > 100 else size.append(100)
plt.xticks(range(2008, 2020, 1))
plt.yticks(range(0, 3200, 200))
plt.scatter(years, turnovers, c=np.random.randint(0, 50, 11), s=size, label='成交额')
plt.plot(years, squares, color='red', label='x^3.4')
plt.plot(years, powers, color='blue', label='2^n')
plt.legend(loc='best', fontsize=16, markerscale=0.5)
plt.xlabel("年份", fontdict={'size': 16})
plt.ylabel("成交额", fontdict={'size': 16})
plt.title("历年天猫双11总成交额", fontdict={'size': 20})
plt.show()

运行结果：

散点图的作用主要是用于分析数据的趋势，用于预测未来的数据。比如我想预测2020年天猫双11的总成交额，通过对比的方式，简单分析一下这个趋势更接近指数函数还是更接近多次函数。

在散点图中，我绘制了两条曲线，y=2^x和y=x^(3.4)，一条是2为底的指数函数，一条是x的3.4次方(三次函数ax^3+bx^2+cx+d)，可以看到双11总成交额的变化趋势更接近三次函数。

这里我只是简单对比一下，三次函数还有二次项、一次项和常数项，所以x^(3.4)中的0.4可以通过二次项、一次项和常数项来补充，指数函数的变化趋势太快，与双11总成交额的变化趋势差异很大。这种简单对比是很粗糙的，只是为了说明散点图可以用于分析趋势。真实的分析不能简单看每年的数据，需要考虑很多因素(甚至因为某个因素的加入，成交额已经快到天花板了，很可能后面会下降)。

总结

到此这篇关于Python利用matplotlib绘制散点图的文章就介绍到这了,更多相关Python matplotlib绘制散点图内容请搜索python博客以前的文章或继续浏览下面的相关文章希望大家以后多多支持python博客！