1. 导入库

import numpy as np #矩阵运算
import matplotlib.pyplot as plt #可视化
import random #产生数据扰动

2. 产生数据

拟合曲线 y = 2 × x² + x + 1 

X_m = np.mat([[i**2, i, 1] for i in range(-10,10)]) #矩阵类型，用于运算
y_m = np.mat([[2*x[0,0]+x[0,1]+1+random.normalvariate(0,1)] for x in X_m]) #矩阵类型，用于运算
X_a = np.asarray(X_m[:,1].T)[0] #array类型，用于可视化
y_a = np.asarray(y_m.T)[0] #array类型，用于可视化
plt.scatter(X_a, y_a) #显示数据
plt.show()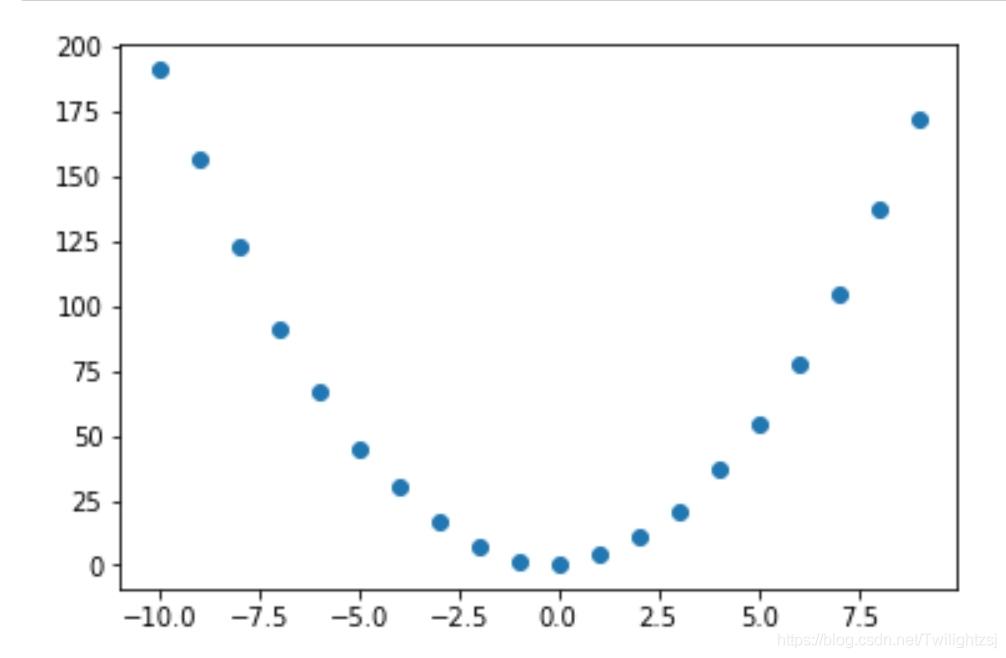

3. BGD

def BGD(X,y,w0,step,e): #批量梯度下降法
  n=0
  while n<=10000:
    w1 = w0-step*X.T.dot(X.dot(w0)-y)/X.shape[0]
    dw = w1-w0;
    if dw.dot(dw.T)[0,0] <= e**2:
      return w1
    n += 1
    w0 = w1
  return w1

4. 计算

w_m = BGD(X_m,y_m,np.mat([[5],[3],[2]]),1e-4,1e-20) #可自行调参
w_a = np.asarray(w_m.T)[0]
print(w_a)

array([1.99458492, 0.91587829, 1.48498921])

5. 评价( R ²)

y_mean = y_a.mean()
y_pre = np.array([w_a[0]*x[0,0]+w_a[1]*x[0,1]+w_a[2] for x in X_m])
SSR = ((y_pre-y_mean)**2).sum()
SST = ((y_a-y_mean)**2).sum()
R2 = SSR/SST
print(R2)

0.9845542903194531
我们可以认为拟合效果不错。如果 R 2 R^{2} R2的值接近0，可能需要重新调参。

6. 结果展示

X = np.linspace(-10,10,50)
y = np.array([w_a[0]*x**2+w_a[1]*x+w_a[2] for x in X])
plt.scatter(X_a,y_a)
plt.plot(X,y)
plt.show()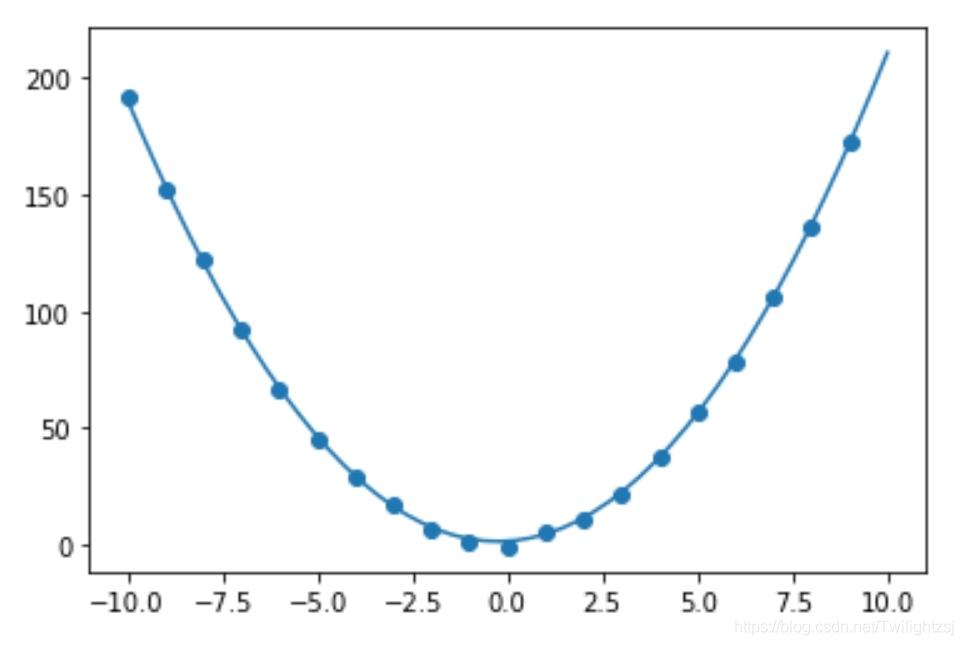

到此这篇关于Python实现批量梯度下降法(BGD)拟合曲线的文章就介绍到这了,更多相关Python 批量梯度下降内容请搜索python博客以前的文章或继续浏览下面的相关文章希望大家以后多多支持python博客！