Python-opencv+KNN求解数独

最近一直在玩数独，突发奇想实现图像识别求解数独，输入到输出平均需要0.5s。

整体思路大概就是识别出图中数字生成list，然后求解。

输入输出demo

数独采用的是微软自带的Microsoft sudoku软件随便截取的图像，如下图所示：

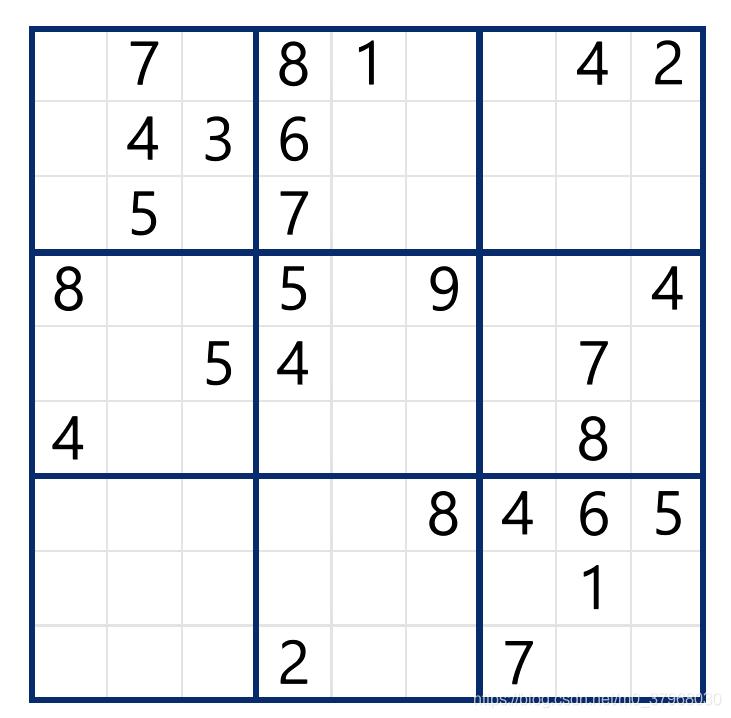
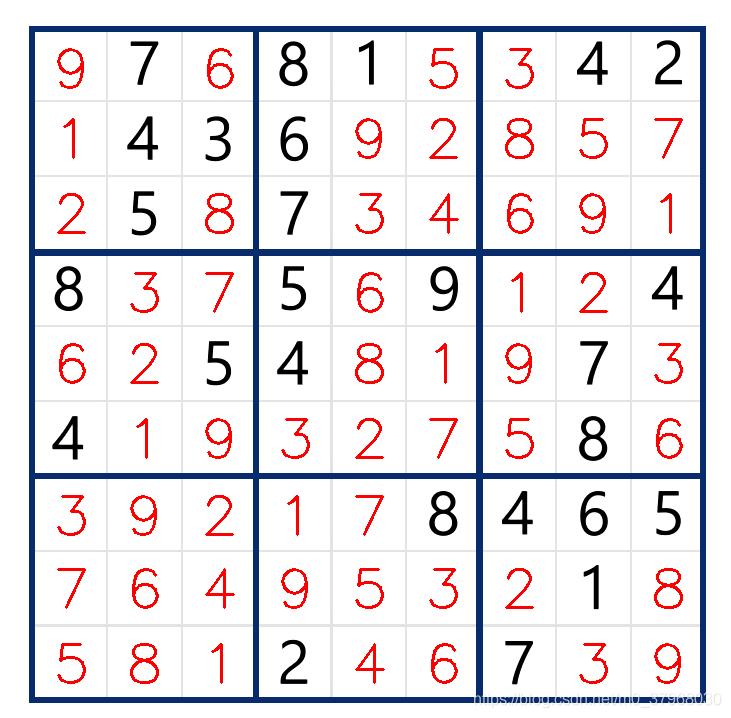
经过程序求解后，得到的结果如下图所示：

程序具体流程

程序整体流程如下图所示：

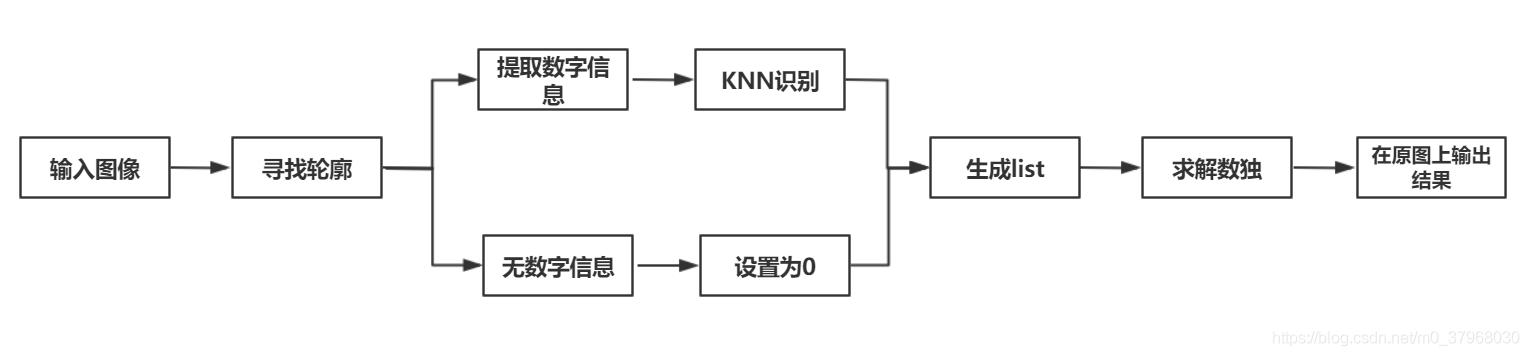
读入图像后，根据求解轮廓信息找到数字所在位置，以及不包含数字的空白位置，提取数字信息通过KNN识别，识别出数字；无数字信息的在list中置0；生成未求解数独list，之后求解数独，将信息在原图中显示出来。

# -*-coding:utf-8-*-
import os
import cv2 as cv
import numpy as np
import time

####################################################
#寻找数字生成list
def find_dig_(img, train_set):
  if img is None:
    print("无效的图片！")
    os._exit(0)
    return
  _, thre = cv.threshold(img, 230, 250, cv.THRESH_BINARY_INV)
  _, contours, hierarchy = cv.findContours(thre, cv.RETR_TREE, cv.CHAIN_APPROX_SIMPLE)
  sudoku_list = []
  boxes = []
  for i in range(len(hierarchy[0])):
    if hierarchy[0][i][3] == 0: # 表示父轮廓为 0
      boxes.append(hierarchy[0][i])
  # 提取数字
  nm = []
  for j in range(len(boxes)):  # 此处len(boxes)=81
    if boxes[j][2] != -1:
      x, y, w, h = cv.boundingRect(contours[boxes[j][2]])
      nm.append([x, y, w, h])
      # 在原图中框选各个数字
      cropped = img[y:y + h, x:x + w]
      im = img_pre(cropped)#预处理
      AF = incise(im)#切割数字图像
      result = identification(train_set, AF, 7)#knn识别
      sudoku_list.insert(0, int(result))#生成list
    else:
      sudoku_list.insert(0, 0)

  if len(sudoku_list) == 81:
    sudoku_list= np.array(sudoku_list)
    sudoku_list= sudoku_list.reshape((9, 9))
    print("old_sudoku -> \n", sudoku_list)
    return sudoku_list, contours, hierarchy
  else:
    print("无效的图片！")
    os._exit(0)

######################################################
#KNN算法识别数字
def img_pre(cropped):
  # 预处理数字图像
  im = np.array(cropped) # 转化为二维数组
  for i in range(im.shape[0]): # 转化为二值矩阵
    for j in range(im.shape[1]):
      # print(im[i, j])
      if im[i, j] != 255:
        im[i, j] = 1
      else:
        im[i, j] = 0
  return im


# 提取图片特征
def feature(A):
  midx = int(A.shape[1] / 2) + 1
  midy = int(A.shape[0] / 2) + 1
  A1 = A[0:midy, 0:midx].mean()
  A2 = A[midy:A.shape[0], 0:midx].mean()
  A3 = A[0:midy, midx:A.shape[1]].mean()
  A4 = A[midy:A.shape[0], midx:A.shape[1]].mean()
  A5 = A.mean()
  AF = [A1, A2, A3, A4, A5]
  return AF


# 切割图片并返回每个子图片特征
def incise(im):
  # 竖直切割并返回切割的坐标
  a = [];
  b = []
  if any(im[:, 0] == 1):
    a.append(0)
  for i in range(im.shape[1] - 1):
    if all(im[:, i] == 0) and any(im[:, i + 1] == 1):
      a.append(i + 1)
    elif any(im[:, i] == 1) and all(im[:, i + 1] == 0):
      b.append(i + 1)
  if any(im[:, im.shape[1] - 1] == 1):
    b.append(im.shape[1])
  # 水平切割并返回分割图片特征
  names = locals();
  AF = []
  for i in range(len(a)):
    names['na%s' % i] = im[:, range(a[i], b[i])]
    if any(names['na%s' % i][0, :] == 1):
      c = 0
    else:
      for j in range(names['na%s' % i].shape[0]):
        if j < names['na%s' % i].shape[0] - 1:
          if all(names['na%s' % i][j, :] == 0) and any(names['na%s' % i][j + 1, :] == 1):
            c = j
            break
        else:
          c = j
    if any(names['na%s' % i][names['na%s' % i].shape[0] - 1, :] == 1):
      d = names['na%s' % i].shape[0] - 1
    else:
      for j in range(names['na%s' % i].shape[0]):
        if j < names['na%s' % i].shape[0] - 1:
          if any(names['na%s' % i][j, :] == 1) and all(names['na%s' % i][j + 1, :] == 0):
            d = j + 1
            break
        else:
          d = j
    names['na%s' % i] = names['na%s' % i][range(c, d), :]
    AF.append(feature(names['na%s' % i])) # 提取特征
    for j in names['na%s' % i]:
      pass
  return AF


# 训练已知图片的特征
def training():
  train_set = {}
  for i in range(9):
    value = []
    for j in range(15):
      ima = cv.imread('E:/test_image/knn_test/{}/{}.png'.format(i + 1, j + 1), 0)
      im = img_pre(ima)
      AF = incise(im)
      value.append(AF[0])
    train_set[i + 1] = value

  return train_set


# 计算两向量的距离
def distance(v1, v2):
  vector1 = np.array(v1)
  vector2 = np.array(v2)
  Vector = (vector1 - vector2) ** 2
  distance = Vector.sum() ** 0.5
  return distance


# 用最近邻算法识别单个数字
def knn(train_set, V, k):
  key_sort = [11] * k
  value_sort = [11] * k
  for key in range(1, 10):
    for value in train_set[key]:
      d = distance(V, value)
      for i in range(k):
        if d < value_sort[i]:
          for j in range(k - 2, i - 1, -1):
            key_sort[j + 1] = key_sort[j]
            value_sort[j + 1] = value_sort[j]
          key_sort[i] = key
          value_sort[i] = d
          break
  max_key_count = -1
  key_set = set(key_sort)
  for key in key_set:
    if max_key_count < key_sort.count(key):
      max_key_count = key_sort.count(key)
      max_key = key
  return max_key


# 生成数字
def identification(train_set, AF, k):
  result = ''
  for i in AF:
    key = knn(train_set, i, k)
    result = result + str(key)
  return result



######################################################
######################################################
#求解数独
def get_next(m, x, y):
  # 获得下一个空白格在数独中的坐标。
  :param m 数独矩阵
  :param x 空白格行数
  :param y 空白格列数
  """
  for next_y in range(y + 1, 9): # 下一个空白格和当前格在一行的情况
    if m[x][next_y] == 0:
      return x, next_y
  for next_x in range(x + 1, 9): # 下一个空白格和当前格不在一行的情况
    for next_y in range(0, 9):
      if m[next_x][next_y] == 0:
        return next_x, next_y
  return -1, -1 # 若不存在下一个空白格，则返回 -1，-1


def value(m, x, y):
  # 返回符合"每个横排和竖排以及九宫格内无相同数字"这个条件的有效值。

  i, j = x // 3, y // 3
  grid = [m[i * 3 + r][j * 3 + c] for r in range(3) for c in range(3)]
  v = set([x for x in range(1, 10)]) - set(grid) - set(m[x]) - \
    set(list(zip(*m))[y])
  return list(v)


def start_pos(m):
  # 返回第一个空白格的位置坐标
  for x in range(9):
    for y in range(9):
      if m[x][y] == 0:
        return x, y
  return False, False # 若数独已完成，则返回 False, False


def try_sudoku(m, x, y):
  # 试着填写数独
  for v in value(m, x, y):
    m[x][y] = v
    next_x, next_y = get_next(m, x, y)
    if next_y == -1: # 如果无下一个空白格
      return True
    else:
      end = try_sudoku(m, next_x, next_y) # 递归
      if end:
        return True
      m[x][y] = 0 # 在递归的过程中，如果数独没有解开，
      # 则回溯到上一个空白格


def sudoku_so(m):
  x, y = start_pos(m)
  try_sudoku(m, x, y)
  print("new_sudoku -> \n", m)
  return m

###################################################
# 将结果绘制到原图
def draw_answer(img, contours, hierarchy, new_sudoku_list ):
  new_sudoku_list = new_sudoku_list .flatten().tolist()
  for i in range(len(contours)):
    cnt = contours[i]
    if hierarchy[0, i, -1] == 0:
      num = new_soduku_list.pop(-1)
      if hierarchy[0, i, 2] == -1:
        x, y, w, h = cv.boundingRect(cnt)
        cv.putText(img, "%d" % num, (x + 19, y + 56), cv.FONT_HERSHEY_SIMPLEX, 1.8, (0, 0, 255), 2) # 填写数字
  cv.imwrite("E:/answer.png", img)


if __name__ == '__main__':
  t1 = time.time()
  train_set = training()
  img = cv.imread('E:/test_image/python_test_img/Sudoku.png')
  img_gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
  sudoku_list, contours, hierarchy = find_dig_(img_gray, train_set)
  new_sudoku_list = sudoku_so(sudoku_list)
  draw_answer(img, contours, hierarchy, new_sudoku_list )
  print("time :",time.time()-t1)

PS：

使用KNN算法需要创建训练集，数独中共涉及9个数字，“1,2,3,4,5,6,7,8,9”各15幅图放入文件夹中，如下图所示。

到此这篇关于Python图像识别+KNN求解数独的实现的文章就介绍到这了,更多相关Python KNN求解数独内容请搜索python博客以前的文章或继续浏览下面的相关文章希望大家以后多多支持python博客！