本文实例为大家分享了python实现梯度下降法的具体代码，供大家参考，具体内容如下

使用工具：Python（x,y） 2.6.6
运行环境：Windows10

问题：求解y=2*x1+x2+3，即使用梯度下降法求解y=a*x1+b*x2+c中参数a，b，c的最优值（监督学习）

训练数据：

x_train=[1, 2], [2, 1],[2, 3], [3, 5], [1,3], [4, 2], [7, 3], [4, 5], [11, 3], [8, 7]

y_train=[7, 8, 10, 14, 8, 13, 20, 16, 28,26]

测试数据：

x_test = [1, 4],[2, 2],[2, 5],[5, 3],[1,5],[4, 1]

# -*- coding: utf-8 -*-
"""
Created on Wed Nov 16 09:37:03 2016
@author: Jason
"""

import numpy as np
import matplotlib.pyplot as plt

# y=2 * (x1) + (x2) + 3 

rate = 0.001
x_train = np.array([[1, 2], [2, 1],[2, 3], [3, 5], [1, 3], [4, 2], [7, 3], [4, 5], [11, 3], [8, 7] ])
y_train = np.array([7, 8, 10, 14, 8, 13, 20, 16, 28, 26])
x_test = np.array([[1, 4],[2, 2],[2, 5],[5, 3],[1, 5],[4, 1]])

a = np.random.normal()
b = np.random.normal()
c = np.random.normal()

def h(x):
 return a*x[0]+b*x[1]+c

for i in range(100):
 sum_a=0
 sum_b=0
 sum_c=0

 for x, y in zip(x_train, y_train):  
  for xi in x:
   sum_a = sum_a+ rate*(y-h(x))*xi
   sum_b = sum_b+ rate*(y-h(x))*xi
   #sum_c = sum_c + rate*(y-h(x)) *1   

   a = a + sum_a
   b = b + sum_b
   c = c + sum_c
   plt.plot([h(xi) for xi in x_test])


print(a)
print(b)
print(c)

result=[h(xi) for xi in x_train]
print(result)

result=[h(xi) for xi in x_test]
print(result)

plt.show()

运行结果：

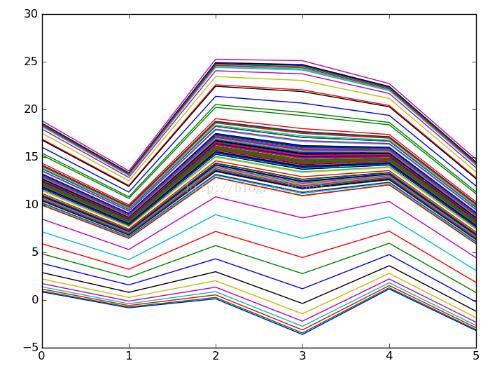
结论：线段是在逐渐逼近的，训练数据越多，迭代次数越多就越逼近真实值。

以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持python博客。